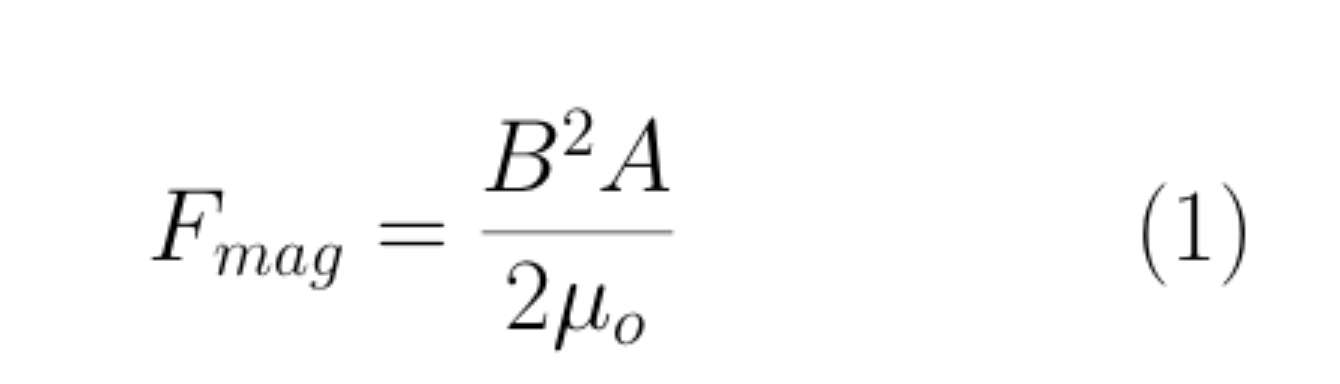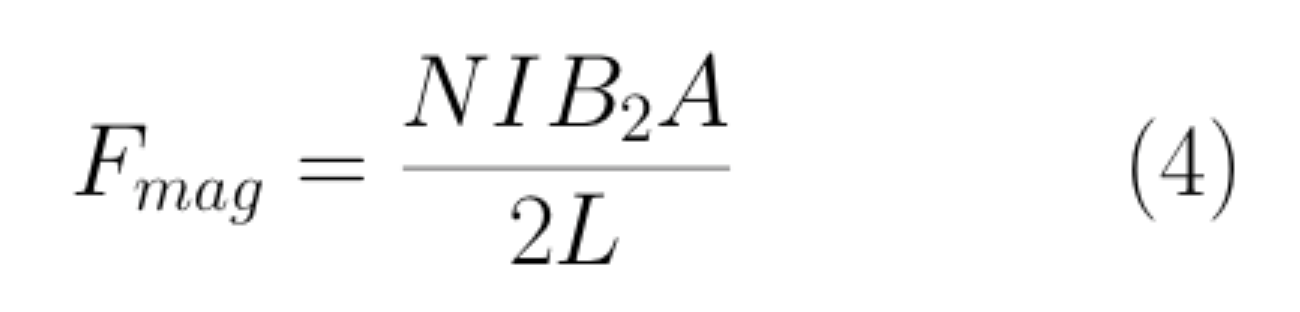¶ Context
This is a bit of a niche subject to talk about. That is because, the only real application for estimating the magnetic force is for the electromagnetic separation. It may prove helpful, for further applications of magnetism, though that is unlikely. All of the calculations displayed here, are all with respect to the diagram below. The electromagnet having N turns and a current I and a length L. The electromagnet is modelled after a solenoid and has a flux density B1. The permanent magnet having a magnetic flux density B2.
¶ General Equation
To model the magnetic force between 2 bodies of the same area A as well as magnetic flux density B, Maxwell's Pulling Force Formula may be used. [1]
By extension of Maxwell's pulling force which assumes that the magnetic flux in the two magnets is the same and hence it squares the quantities. Therefore, B 2 can be rewritten as B 1 B 2 , where B 2 is obtained when B 1 = B 2 = B. This creates equation (2).
Now, it is possible to calculate the magnetic force between 2 magnets. From Newton's third law, the attractive force between two magnets should be the same as the repulsive force. This means that the magnitude F mag is for both repulsion and attraction. Therefore, to completely describe the situation, the magnetic flux density in the solenoid is also required.
¶ Solenoid Magnetic Flux Density
To estimate B in a solenoid, equation (3) can be used. This equation calculates the magnetic flux density with the number of turns N, the current passing through it I and the length L.
¶ Rearranging Together
By substituting equation (3) into equation (2), a formula is obtained that allows calculation of magnetic flux density between a solenoid and a permanent magnet.
[1] http://info.ee.surrey.ac.uk/Workshop/advice/coils/force.html [accessed 1 December 2020]
[2] https://www.omnicalculator.com/physics/solenoid-magnetic-field#solenoid-magnetic-field-equation [accessed 5 December 2020]