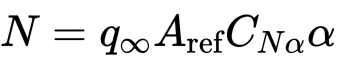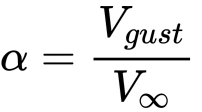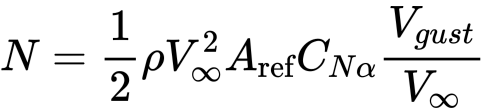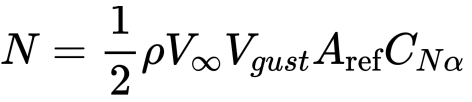¶ Objective
To estimate the bending moment and shear in a rocket.
¶ Assume:
- Simple Beam theory
-
Assume clamped nose cone or clamped fins = Ignore accelerations (which should be the worst case)
- Ignore the inertia of the rocket/mass components
- Ignore gravitational forces
- Lift coefficients from the fins can be found from openRocket
- Worst case is due to a gust of magnitude 9 m/s (based on Aspire Space paper)
¶ Method:
- Calculate the lift from the fins
- Assume this is a point load at the fins centre of pressure
- Assume the nose cone is fixed, so it behaves like a cantilevered beam
- Get the shear and bending moment distribution from simple beam theory
¶ Estimate the lift from the fins:
Open Rocket gives an estimate from CNalpha in the component analysis tab.
CNalpha is = C_N/alpha and CN is the normal force due to some angle of attack, and this is the lift force that will contribute to the bending moment.
For sporadic Impluse, CNalpha = 6.35 at the fins and CNalpha = 2. Therefore for any given angle of attack, the fins are going to create a larger bending moment when the nose is clamped compared to the other case. So we focus on the nose clamped, fins at angle of attack case.
by small angle approximation
therefore
and we can see that the N is proportional to the Vinfty and gust speed.
¶ Bending Moment due to a point load:
Assuming cantilevered beam of length L, and x measured from the nose cone downwards.
M(x) = N (L-x)
and S(x) = N
¶ Example
For Sporadic Impulse on 8 Feb 2020:
- Aref = pi*3inch^2 = 0.01767 m^2
- Vgust = 9 m/s
- Vinf (max) = 250 m/s
- CNa = 6.35 (from openRocket)
- rho = 1.225
- L = 4 m
Therefore the N = 0.5*1.225*250*9*0.01767*6.35 = 154.6 N
Therefore M(x) = 154.6*(4 - x)
Therefore:
| x (measured from the nose) (m) | Moment Arm (m) | M(x) (Nm) | M(x) * Safety factor of 2 (Nm) |
|---|---|---|---|
| 0 | 4 | 618 | 1236 |
| 1 | 3 | 464 | 927 |
| 2 | 2 | 309 | 618 |
| 3 | 1 | 155 | 309 |
and the shear force is always the lift force, so S(x) = 154.6 N, and with a safety factor of 2, S(x)*SF = 309 N