¶ Program Architecture
The current iteration of the simulator is written in Python and organised as follows:
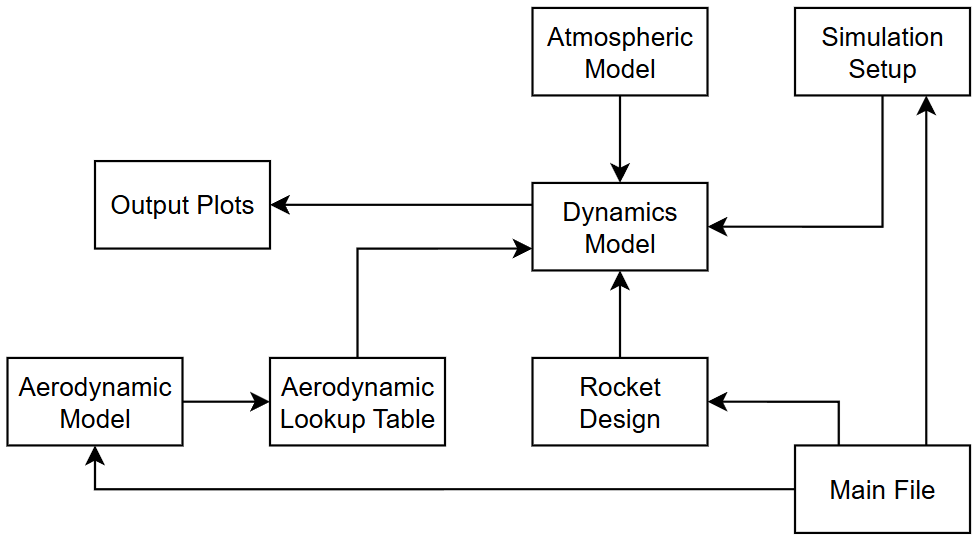
Data flow within the program
The main parts of the program which require extra information are explained more in-depth below, with derivations and resources for understanding specific parts of the code also given.
¶ Atmospheric Model
Wind and IFFT
¶ Aerodynamics Model
ESDU is the best lol
¶ Dynamics Model
The model works as follows:
- Initial conditions for the simulation, rocket, and atmosphere are generated from the required files.
- The function which takes in a state and returns its derivative is run - this is where all the maths happens.
- RK4 is used to integrate this over time.
- Plots are generated at the end of the flight using data returned from the main function.
The two most complex parts of the program - the state derivative calculation and the numerical integration - are explained below:
¶ State recalculation
The state vector of the rocket consists of 5 quantities:
where represents the rocket’s position (and its time derivative); the quaternion representing the transformation between the earth frame and body frame; the angular velocity vector, and the current mass of the rocket. This is then enough information to recalculate the subsequent value of the state vector given the extra information provided such as rocket geometry and atmospheric conditions. Now we will proceed with calculating the derivative of each of these quantities in turn.
¶ The easiest part - calculating
This is already a state input so there’s no calculation to do here. If you really want an equation,
Incredible.
¶ Translational dynamics - calculating
This is very similar to the procedure in simulators with lower degrees of freedom, and the forces are simply added to obtain the acceleration.
The two main things here which cause some difficulty is determining the value of (from the aerodynamics model) and the conversion in axis systems required to add the forces - for example, is most easily obtained in the earth frame of reference, but is from the body frame, and is most simple in the inertial frame. This is handled with quaternions for computational efficiency, explained in the next section.
¶ Rotational dynamics in the fourth dimension - calculating
This is probably the hardest thing to understand in this code, so if you want to just trust the equations then fair enough. Here’s a brief explanation of what is going on:
- The quaternion represents a transformation from the earth frame of reference to the body frame. For example, a value of 1 represents the identity and would be used if the earth axes and body axes are equivalent (i.e. the rocket is pointing straight up).
- At each timestep, the angular velocity is converted into a purely imaginary quaternion .
- This can then be used to get the quaternion derivative using the equation
using quaternion multiplication. The derivation of this is quite involved, details can be found here.
¶ Rotational dynamics you can actually understand - calculating
The way in which is obtained is very similar to the translational dynamics - but instead of summing forces, the resultant moment is found.
¶ Engine calculations - calculating
¶ Numerical integration
¶ Other parts
- ???